Diagramas de espacio-tiempo de Minkowsky

En física clásica, la coordenada del tiempo no es afectada por una transformación de un sistema inercial a otro. La coordenada del tiempo, t', de un sistema inercial no depende de las coordenadas espaciales, x, y, z de otro sistema inercial, siendo la ecuación de transformación t' = t. Sin embargo, en relatividad, el espacio y el tiempo son interdependientes. La coordenada del tiempo de un sistema inercial depende tanto del tiempo como de la coordenada espacial del otro sistema inercial, siendo la ecuación de transformación:

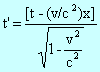
A continuación, se considerará solamente un eje espacial, el eje x y se ignorarán los ejes y y z. No se perderá generalidad por esta simplificación algebraica y este procedimiento permitirá enfocar mas claramente la interdependencia del espacio y el tiempo y su representación geométrica. Entonces, las coordenadas de un evento están dadas por x y t. Todas las coordenadas espacio-tiempo pueden representarse en un diagrama espacio-tiempo en el que el eje del espacio sea horizontal y el eje del tiempo sea vertical. Es conveniente conservar las dimensiones de las coordenadas iguales; esto se hace fácilmente multiplicando el tiempo t por la constante universal c, la velocidad de la luz. Se representara c·t por el símbolo w. Luego, las ecuaciones de transformación de Lorentz pueden escribirse como sigue:

Nótese la simetría en esta forma de las ecuaciones.

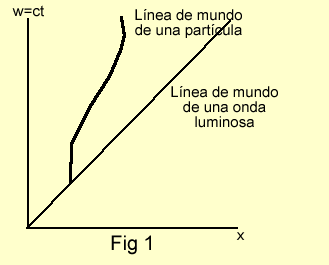Para representar la situación geométricamente, se comienza trazando los ejes x y w del sistema O ortogonales (perpendiculares) entre si (Figura1). Si se desea representar el movimiento de una partícula en este sistema, se traza una curva, denominada línea de mundo, que da el lugar geométrico de los puntos espacio-tiempo correspondientes al movimiento. La tangente a la línea de mundo en cualquier punto, es dx/dw = – (dx/dt), y esta inclinada con respecto al eje de tiempo en un ángulo que es menor de 45º. Ello se debe a que este ángulo esta dado por tgθ = dx/dw = u/c y se debe tener u < c para una partícula material. La línea de mundo de una onda de luz, para la cual u = c es una recta que hace un ángulo de 45º con los ejes.

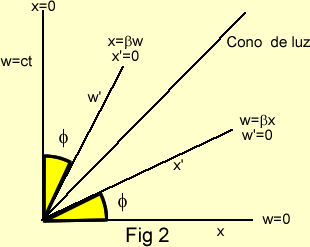Se considera ahora el sistema (O') que se mueve con respecto a O, desplazándose a una velocidad v a lo largo del eje común x-x'. La ecuación de movimiento de O' con respecto a O puede obtenerse haciendo x' = 0 (lo cual localiza el origen de O'); de la ecuación se nota que esto corresponde a x = βw (= vt). Se traza la línea x' = 0 (es decir x = βw) en el diagrama (Fig. 2) y considerando que v < c y 0 < 1, el ángulo que esta línea hace con el w, Φ = (tg^-1β), es menor que 45º. Del mismo modo que el eje w corresponde a x = 0 y es el eje del tiempo en el sistema O, así la línea x' = 0 da el eje del tiempo w' en O'. Ahora, si se traza la línea w' = 0 (dando la localización de relojes que leen t' = 0 en O'), se tendrá el eje espacial x'. Es decir, de la misma manera que el eje x corresponde a w = 0, así el eje x' corresponde a w' = 0. Pero, de la ecuación, w' = 0 significa que w = βx es la ecuación de este eje en el diagrama w – x (Fig.2). El ángulo entre los ejes espaciales es el mismo que el de los ejes temporales. 

Minkowski se refiere al espacio-tiempo como “el mundo”. Por lo tanto, los eventos son puntos del mundo y un conjunto de eventos que la historia de una partícula es una línea de mundo. Las leyes físicas de la interacción de las partículas se consideran corno las relaciones geométricas entre sus líneas de mundo. En este sentido, se puede decir que Minkowski ha geometrizado la física.

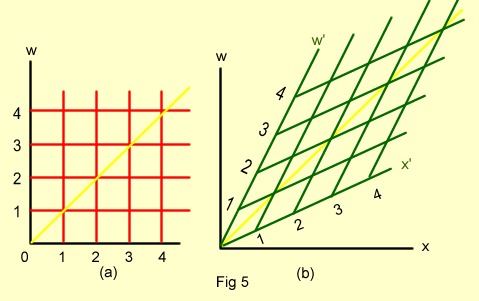
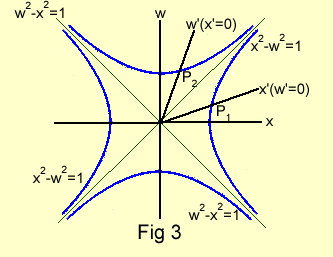Por simplicidad, se estudia solamente el cuadrante en el cual x y w son positivos. Una onda de luz que avanza a mayores valores de x a medida que pasa el tiempo biseca los ejes x-w tanto del tercer cuadrante (donde x y w son ambos negativos) como del primer cuadrante. Una onda de luz que avanza a menores valores de x y del tiempo bisecta los ejes x-w en los cuadrantes segundo y cuarto. (Ver, por ejemplo, las líneas verdes de la Fig.3). Sustracciones y adiciones similares se aplican a la línea de mundo de una partícula y a los ejes del sistema O' cuando se usan coordenadas de espacio-tiempo negativas o cuando el sistema O' se desplaza en la dirección opuesta a la de O.

De la Fig.2, se nota que en el espacio en cuatro dimensiones (x,y,z,t) las ecuaciones de Lorentz, implican la transformación de un sistema ortogonal a un sistema no ortogonal. Se puede usar esta representación para mostrar la relatividad de la simultaneidad y dar una interpretación geométrica de los efectos de contracción del espacio y de dilatación del tiempo, así como ilustrar su naturaleza recíproca. Para hacer esto con claridad, se representara en primer lugar la situación en un nuevo diagrama. (Fig.3). Aquí se trazan las dos ramas de la hipérbola w² – x² = 1 y las dos ramas de la hipérbola x² – w² = 1. Estas líneas cuyo significado será pronto claro, se aproximan de forma asintótica a las líneas de mundo, a 45º, del haz de luz. Se trazan también los ejes x, w de O y los ejes x', w' de O'.

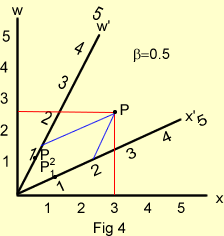
 El punto espacio-tiempo P, es la intersección de la rama derecha de la hiperbola x² – w² = 1 con el eje x' dado por w = βx. Luego, P₁, se encuentra en ambas líneas y sus coordenadas (obtenidas combinando las ecuaciones de las líneas) son:

 Pero, la comparación de las ecuaciones A-2 y A-1 muestra que la primera representa la unidad de longitud (es decir, x' = 1) y el tiempo cero (es decir, w' = 0) en el sistema O' . Esto es, el intervalo OP, de la unidad de longitud en el eje x'. Similarmente el punto espacio-tiempo P₂ es la intersección de la rama superior de la hipérbola w² – x² = 1 con el eje w' dado par x = βw. Luego P, se encuentra en ambas líneas y sus coordenadas (obtenidas combinando las ecuaciones de las líneas) son

 La comparación de las ecuaciones A-3 y A-1 muestra que la primera representa la unidad del tiempo (es decir, w' = 1) y la longitud cero (es decir, x' = 0) en el sistema O' . Esto es, el intervalo OP₂ da la unidad de longitud a lo largo del eje w'.

 A menudo se hace referencia a las hipérbolas como curvas de calibración. Por ejemplo, se considera la hipérbola superior. Para x = 0, se tiene w = 1, que (en unidades de ct) es la unidad de tiempo en O. En cualquier otro punto x se tiene c²t² – x² = c² (t² – x²/c²) = c² τ² = 1. Así, los puntos en la hipérbola superior nos proporcionan la unidad de tiempo en el reloj en reposo en O' , es decir, el tiempo propio en unidades de cτ es igual a uno. Cualquiera que sea la velocidad relativa de O' con respecto a O, la intersección del eje del tiempo con esta hipérbola dará la unidad de tiempo en O' . De modo semejante, para la hipérbola de la derecha se tiene x = 1 para w = 0, que es la unidad de longitud en O (medida a partir del origen). Para cualquier otro valor de w, los puntos sobre la hipérbola representan la unidad de longitud en reposo en un sistema O' , y la velocidad de O' respecto a O está determinada por la inclinación del eje del espacio que cruza a la hipérbola en el punto en cuestión.

Ahora se supone que se observan eventos desde dos sistemas inerciales O y O' , cuya velocidad relativa se conoce. Las curvas de calibración hiperbólica determinan los intervalos de unidad de tiempo y de unidad de longitud sobre los ejes de estos sistemas; una vez que se han usado las hipérbolas se las puede dejar de lado. En la Fig.4 se muestra la calibración de los ejes O y O' , siendo el intervalo de unidad de tiempo a lo largo de w' mayor que el de la unidad de tiempo a lo largo de w y el intervalo de longitud a lo largo de x' mayor que el de la unidad de longitud a lo largo de x.

 

Lo primero que se debe hacer es determinar las coordenadas espacio-tiempo de un evento, tal como P, del diagrama de Minkowski. Para encontrar la coordenada espacial del evento, se traza simplemente una línea paralela al eje del tiempo desde P hacia el eje del espacio. La coordenada del tiempo también está dada por una línea paralela al eje del espacio trazada desde P hacia el eje del tiempo. Estas reglas se cumplen tanto para el sistema O' como para el sistema O. Por ejemplo, en la Fig.4, el evento P tiene coordenadas espacio-tiempo x = 3, w = 2.5 en O (líneas cortas), y coordenadas espacio-tiempo x' = 2, w' = 1.5 en O' (líneas punteadas). Es como si el sistema rectangular de coordenadas de O (figura.5a) se comprimiera hacia la línea bisectriz de 45º cuando las líneas de coordenadas de O' se colocan en el mismo gráfico. (Fig.5b); obviamente, las ecuaciones de transformación de Lorentz transforman un sistema ortogonal en uno no ortogonal.